神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
神经元的作用:接收n个输入信号 -> 带权重的连接(connection) -> 神经元将总输入值与阈值比较 -> 通过激活函数(activation function)处理(决定抑制或激活)-> 产生一个输出信号
理想激活函数为阶跃函数: $x\geq0$时输出1,$x<0$时输出0。然而阶跃函数不连续,不光滑,因此常用Sigmoid函数替代。
Sigmiod函数,译作「形似S的函数」,典型代表为$f(x)=\frac{1}{1+e^{-x}}$ .
目前只需将神经网络视为包含了许多参数的数学模型,模型由若干个函数(例如$y_j=f(\Sigma_i w_ix_i -\theta_j)$ )嵌套代入而得。常见的神经网络是多层前馈结构,「前馈」并不意味着网络中信号不能向后传,而是指网络拓扑结构上不存在环或回路。
对于式$y_j=f(\Sigma_i w_ix_i -\theta_j)$,$x_i$表示上一层第$i$个神经元的输入值,$w_i$是与之对应的权重,$y_j$表示当前层第$j$个神经元的输出值,$\theta_j$为该神经元的阈值。
常见的训练过程:
- 定义一个神经网络(初始化)
- 读取输入数据集
- 通过网络进行计算
- 计算输出值和实际值的误差
- 使用反向传播(Back Propagation)算法更新权值
- 迭代
反向传播算法的简单介绍可参考2017 CS231n-4笔记
若使用用反向传播算法训练多层(三个以上的隐层)神经网络,误差的发散会导致网络难以收敛到稳定状态。通常采用以下两种方式进行训练:
- 逐层训练(预训练)+微调
- 权共享
而卷积神经网络则主要使用权共享策略进行,即每层的多通道间采用相同的权值。
数据导入
torchvision的数据库中提供了MNIST的数据集,并可直接下载。
加载图像后,通常需要对图像进行若干预处理。比如减去RGB通道的均值,或者裁剪或翻转图像实现数据增强等,这些操作可以在torchvision.transforms包中找到对应的操作。在下面的代码中,通过使用transforms.Compose(),我们构造了对数据进行预处理的复合操作序列。
Pad(2)将原始数据集中的$2828$转换为$3232$,便于按照LeNet的网络定义实现。ToTensor负责将PIL图像转换为Tensor数据(RGB通道从[0, 255]范围变为[0, 1]);Normalize负责对图像进行规范化,通过指定均值mean和标准差std,将输入转化为input[channel] =(input[channel] - mean[channel]) / std[channel]
import torch
import torch.nn as nn
from torch.autograd import Variable
import torchvision.datasets as dset
import torchvision.transforms as transforms
import torch.nn.functional as F
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
import time
trans = transforms.Compose([transforms.Pad(2), transforms.ToTensor(), transforms.Normalize((0.5,), (1.0,))])
# Load MNIST dataset(Download if not exist)
train_set = dset.MNIST(root='./MNIST', train=True, transform=trans, download=True)
test_set = dset.MNIST(root='./MNIST', train=False, transform=trans)
# Batch size and number of rounds(epoch)
batch_size = 128
round = 30
# model selection: 0 - MLP; 1 - LeNet
mFlag = 1
train_loader = torch.utils.data.DataLoader(dataset=train_set, batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_set, batch_size=batch_size, shuffle=False)
多层感知机
首先搭建一个简单的感知机网络进行测试。输入层为图像数据,即32*32个神经元,隐藏层300个神经元(可以手动任意指定),输出层为10个类别。
class MLPNet(nn.Module):
def __init__(self):
super(MLPNet, self).__init__()
self.fc1 = nn.Linear(32*32, 300)
self.fc2 = nn.Linear(300, 10)
def forward(self, x):
x = x.view(-1, 32*32)
x = self.fc2(x)
return x
LeNet
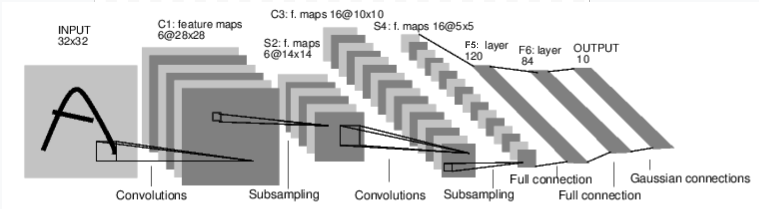
可直接参考PyTorch官方教程NEURAL NETWORKS.
此处额外添加特征可视化的操作,我们选择对C3层(即大小为10*10的卷积层)的结果进行可视化。
# Define LeNet
class LeNet(nn.Module):
# Structure
def __init__(self):
super(LeNet, self).__init__()
# 1 input image channel, 6 output channels, 5x5 square convolution
# kernel
self.conv1 = nn.Conv2d(1, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
# an affine operation: y = Wx + b
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
# Forward computing
def forward(self, x):
# Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:] # all dimensions except the batch dimension
num_features = 1
for s in size:
num_features *= s
return num_features
# Feature visualization for the 10*10 conv layer
def get_feature_map(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2, 2)
x = F.relu(self.conv2(x))
return x
训练和测试
固定套路进行。参考文章toy demo - PyTorch + MNIST
# optimizer & loss function
optimizer = optim.SGD(model.parameters(), lr=0.01)
criterion = nn.CrossEntropyLoss()
model.eval()
# Save the last epoch weights into array.
feature_map = []
# Save the accuracy into an array, then plot curves.
acc_arr = []
for epoch in range(round):
# trainning
ave_loss = 0
for batch_idx, (x, target) in enumerate(train_loader):
optimizer.zero_grad()
x, target = Variable(x), Variable(target)
# Feature visualization
if mFlag == 1 and epoch == round-1 and batch_idx == 0:
feature_map.append(model.get_feature_map(x))
out = model(x)
loss = criterion(out, target)
# weighted sum of old loss and new loss
ave_loss = ave_loss * 0.9 + loss.data * 0.1
loss.backward()
optimizer.step()
if (batch_idx + 1) % batch_size == 0 or (batch_idx + 1) == len(train_loader):
print('Epoch: {}, Index: {}, Loss: {:.3f}'.format(epoch, batch_idx + 1, ave_loss))
# testing
correct_cnt, ave_loss = 0, 0
total_cnt = 0
with torch.no_grad():
for batch_idx, (x, target) in enumerate(test_loader):
x, target = Variable(x), Variable(target)
out = model(x)
loss = criterion(out, target)
_, pred_label = torch.max(out.data, 1)
total_cnt += x.data.size()[0]
# predict equals to real value.
correct_cnt += (pred_label.detach().cpu().numpy() == target.data.detach().cpu().numpy()).sum()
# smooth average
ave_loss = ave_loss * 0.9 + loss.data * 0.1
if (batch_idx + 1) % batch_size == 0 or (batch_idx + 1) == len(test_loader):
acc = correct_cnt * 1.0 / total_cnt
acc_arr.append(acc)
print('Epoch: {}, Index: {}, Test loss: {:.3f}, acc: {:.3f}'.format(epoch, batch_idx + 1, ave_loss, acc))
精度曲线和特征可视化
以轮数(round)为横轴,精度(accuracy)为纵轴,调用matplotlib的相关函数,绘制精度随训练轮数变化的折线图。
round_n= np.arange(round)
plt.title('Accuracy')
plt.xlabel('Epoch(n)')
plt.ylabel('Acc(%)')
plt.plot(round_n, acc_arr, 'b')
plt.grid()
plt.show()
多层感知机(最终准确率93.5%):

LeNet(最终准确率98.6%):

接下来,将权重数值转存为图像。
# extract features
feature_map[0] = feature_map[0].data.cpu().numpy()
feature_map_plot = np.zeros((feature_map[0].shape[0],feature_map[0].shape[2],feature_map[0].shape[3]))
for channels in range(feature_map[0].shape[1]):
feature_map_plot += feature_map[0][:,channels,:,:]
for samples in range(feature_map[0].shape[0]):
arr = np.zeros((feature_map[0].shape[2],feature_map[0].shape[3]))
arr = feature_map_plot[samples]
plt.matshow(arr, cmap='Greys')
figure_name = "Features/" + str(samples) + ".png"
plt.savefig(figure_name)
plt.close()

可以从这些特征图像中隐约看到一些数字的轮廓。
小结
MNIST数据集的处理、训练和测试的过程可以看作对于神经网络理论的一个最初步的实现。整份代码中最关键的部分就是网络结构的搭建。
CNN相对传统多层感知机具有明显的优越性。但深度神经网络仍然是难以解释的「黑箱模型」,且训练时间较长。
本文概念部分主要参考了「周志华. 机器学习. 清华大学出版社, 2016. 9」第五章内容,部分代码来源和细节问题已在文中注明出处。